Himpunan Matematika

Himpunan Matematika

Jenis Himpunan

Jenis	Notasi	Keterangan
Himpunan A yang anggota-anggotanya semua huruf kecil dalam abjad (latin).	A = {a, b, c, ...}	A  adalah nama yang diberikan kepada suatu himpunan
Himpunan yang anggotanya sama banyak	A R B	A = {1, 2, 3, 4} B = {a, b, c, d} Banyaknya anggota A = 4 ditulis n(A) = 4. Banyaknya anggota B = 4, ditulis n(B) = 4. n(A) = n(B) = 4
Himpunan yang sama	A = B	Himpunan A dikatakan sama dengan himpunan B bila setiap anggota A juga menjadi anggota B dan sebaliknya.
Himpunan kosong	{  } atau Ø	Himpunan yang tidak mempunyai anggota sama sekali.
Himpunan bagian	A  T  B	A himpunan bagian dari himpunan B.
Himpunan universum atau semesta pembicaraan	U atau S	Adalah himpunan dari semua unsur yang dibicarakan.
Himpunan komplemen	A’ Atau Ac	U = {1, 2, 3, 4, 5, 6}. A = {3, 5} A’ = Ac = himpunan komplemen dari A = {1, 2, 4, 6}
Himpunan lepas (disjoint)	A  || B	Himpunan A lepas dari himpunan B bila tidak ada anggota A yang menjadi anggota B.

Operasi Himpunan

Jenis Operasi		Hukum dan sifat-sifat Operasi
1	Gabunan (Union)	A U B = B U A disebut sifat komutatif gabungan (A U B) U C = A U (B U C) disebut sifat asosiatif gabungan A U Ø = A A U U = U A U A = A A  U A’ = U Disebut sifat komplemen gabungan
2	Irisan (intersection)	A W B = B W A disebut sifat komutatif irisan A W A = A A W  = Ø A W U = A A W A’ = Ø disebut sifat komplemen irisan (A W B) W C = A W (B W A) disebut sifat asosiatif irisan
2	Distributif	A U (B W C) = (A U B) W (A U C); disebut sifat distributif gabungan terhadap irisan. A W (B U C) = (A W B) U (A W C); disebut sifat distributif irisan terhadap gabungan.
3	Selisih	A – A = Ø A – Ø = A A – B = A W B’ A – (BUC) = (A – B)W (A – C) A – (B W C) = (A – B)U(A – C)
4	Komplemen	(A’)’ = A U’ = Ø Ø’ = U AUA’ = U AWA’ = U AWA’= Ø
5	Banyaknya Anggota	n(A) + n(B) K n(AUB) n(AUB) = n(A) + n(B) – n(AWB) n(AUBUC) = n(A) + n(B) + n(C) – n(AWB) – n(BWC) – n(CWA) + n(AWBWC) n(A) + n(B) = n(AUB) + n(AWB) n(A) + n(B) + n(C) =n(AUBUC) + n(AWB) + n(AWC) + n(BWC) – n(AWBWC)

Diagram Venn

Pernyataan		Diagram
1	Himpunan Semesta U
2	U = {1,2,3,4,5,6,7,8,9}
3	ATU
4	ATU BTA BTU
5	A = B
6	CTBTATU Contoh {Bilangan Asli} A = {1,2,3,... 10} B = {1,3,5,9} C = {1,3}

Operasi		Diagram
Gabungan Himpunan	A = {a,b,c,d} B = {e,f} A U B = {a,b,c,d,e,f,}
	A = {1,2,3,4} C = {3,4,5} A U C = {1,2,3,4,5}
	E = {x,y,z} F = {x} E U F = {x,y,z}
Irisan	A = {a,b,c,d} B = {c,d,e} A W B= {c,d}
	C = {a,b,c,d} D = {a,b} C W D = {a,b}
	E = {a,b,c} F = {1,2,3} E W F = { Ø }
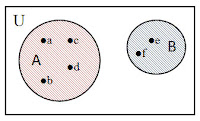
Selisih Himpunan	A = {a,b,c} B = {d,e} A / B = {a,b,c}
	C = {1,2,3} D = {3,4} C / D = {1,2}
	D / C = {4}
Himpunan Komplemen	A’ atau komplemen dari A
	(A W B)’ = A’ U B’
	A’ W B’ = (AUB)’

Perkalian Himpunan (Cartesian Product)

Perkalian Himpunan (Cartesian Product)

Notasi:

A x B = ...???

A = {a,b,c}

B = {p,q}

A x B = {(a,p),(a,q),(b,p),(b,q),(c,p),(c,q)}

Tambahan:
Bagi yang bingung, berikut bagan Perkalian Himpunan (Cartesian Product) (Kanan).

Catatan:

(a,b) = (a,b)

(a,b) K (b,a)